Going Deeper:  Molecular vibrations:

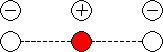
A molecule has 3N-6 vibrations associated with it, where N is the number of atoms.  The 6 motions that are subtracted correspond to 3 translational and 3 rotational motions with zero frequency.  A linear molecule has 3N-5 vibrations, because one of the rotational motions is lost due to the symmetry of the molecule.  In the case of a non-linear triatomic molecule ABA, similar to H₂O, the three normal modes of vibration are:  symmetric stretching, symmetric bending and anti-symmetric bending (Fig 9.4) .  For a linear triatomic, 4 modes of vibration are predicted.  In contrast to the non-linear triatomic, a linear triatomic molecule has an anti-symmetric stretching mode of vibration. (Fig 9.5) 

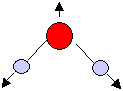	Symmetric stretching mode
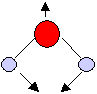	Symmetric bending mode
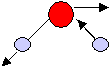	Antisymmetric bending mode
Fig 9.4 The 3 modes of vibration of a non-linear triatomic molecule ABA (i.e. H2O)

Raman Spectrum of CO2
n1
n3
n2a
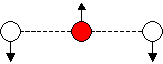n2b
FIG 9.5  The 4 modes of vibration of a linear triatomic molecule

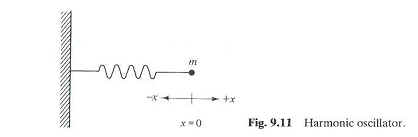
Fig 9.11 Diatomic molecule:  vibration is similar to motion of two atoms linked by a spring

Each mode of vibration has a frequency of oscillation associated with it.  For a diatomic molecule, a good analogy is a mass connected to a wall by a spring (Fig 9.11).  This would be similar to a molecule like HCl or HBr, where the hydrogen atom is much lighter than either Cl or Br.  In the absence of any forces, the mass on the spring is at its equilibrium position – the length of the spring at rest.  If we stretch or compress the spring from its equilibrium position, then classically we can talk about a restoring force associated with the spring that will bring the mass back to its equilibrium position.  This strength of this restoring force will be dependent on the relative stiffness of the spring, which can be described by a force constant.  In the case of a bond, the force constant describes the relative strength of a bond so, for example, a double bond will have a larger force constant than a single bond.  Classically, force, F=ma (mass ´ acceleration) and in the case of our spring, 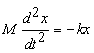, where k is the force constant and x is the displacement from the equilibrium position.  If we solve for x, then .  From this relationship, we know that the frequency of a vibration is directly related to the force constant of the bond and inversely related to the masses of the interacting atoms.  For molecules bigger than diatomics the coupling of motions with other atoms or vibrations also needs to be considered.

Back to Top

(What is Raman Spectroscopy?)

Previous | Next

(UVRR on HbA & HbS tetramers)